The Multiplicative Axis: A New Approach to Navier-Stokes with Prime Number Gates

mindmap
  root((Multiplicative_Axis_Framework))
    Core_Philosophy
      Geometric_Gating
      Physics_as_Lens
      Manifold_Optimization
    Mathematical_Engine
      Prime_Indexed_Constraints
      Euler_Product_Gates
        Attenuation
        Soft_Zeros
      Exponential_Barriers
        Amplification
        Hard_Walls
    Historical_Roots
      FDE_Solver_2016
      Haar_Wavelets
      Multi_Resolution_Analysis
      Structured_Decomposition
    Validation_Navier_Stokes
      Stability_8000_Steps
      High_Frequency_Capture
      Gradient_Orthogonality_Solved
      Turbulence_Preservation

Introduction: The Challenge of Convergence

The promise of Physics-Informed Neural Networks (PINNs) is notable: a universal approximator that not only learns from data but obeys the fundamental laws of nature. However, the reality of training these networks is often a struggle against gradient pathology.

In the standard formulation, physical laws are treated as soft penalties added to the loss function:

\[ \mathcal{L}_{total} = \mathcal{L}_{data} + \lambda \cdot \mathcal{L}_{physics} \]

While theoretically sound, this additive coupling creates a multi-objective optimization problem where the objectives are often conflicting. In complex systems like fluid dynamics (Navier-Stokes), the gradients of the data loss (\(\nabla \mathcal{L}_{data}\)) and the physics loss (\(\nabla \mathcal{L}_{physics}\)) can point in nearly orthogonal directions. The network, seeking the path of least resistance, often minimizes the physics loss by smoothing out high-frequency features—effectively “cheating” the differential equation to satisfy the easier data fitting task.

We suggest that this may not be a failure of the network, but a limitation of the additive topology. Physics is not just a penalty to be minimized; it can be viewed as a manifold to be inhabited.

The Multiplicative Axis Hypothesis

At ShunyaBar Labs, we propose a paradigm shift from additive penalties to multiplicative gating. We hypothesize that physical constraints should act as a “lens” through which the data loss is viewed.

\[ \mathcal{L}_{total} = \mathcal{L}_{data} \cdot \Phi(\mathcal{L}_{physics}) \]

Here, \(\Phi\) is a Constraint Functional that acts as a gate. * If the physics is violated (\(\mathcal{L}_{physics} > \epsilon\)), \(\Phi\) explodes, rendering the data loss irrelevant and forcing the optimizer to return to the physical manifold. * If the physics is satisfied (\(\mathcal{L}_{physics} \approx 0\)), \(\Phi\) approaches unity, allowing the network to focus purely on data assimilation.

This multiplicative coupling ensures that gradient flow is modulated by physical validity. The network cannot learn from data unless it is simultaneously respecting the laws of physics.

Theory: Prime-Indexed Geometry

To implement this functional \(\Phi\) robustly, we draw inspiration from Analytic Number Theory. We require a system that can handle multiple, potentially conflicting constraints (e.g., conservation of mass, conservation of momentum, energy bounds) without interference.

Euler Product Gates (Attenuation)

We map each distinct physical constraint \(C_i\) to a prime number \(p_i\). The attenuation gate \(G(v)\) is constructed as a truncated Euler product:

\[ G(\mathbf{v}) = \prod_{i} (1 - p_i^{-\tau v_i}) \]

where \(v_i\) is the violation magnitude of the \(i\)-th constraint. This structure provides hierarchical orthogonality. Just as the Fundamental Theorem of Arithmetic guarantees that integers have a unique prime factorization, this mapping ensures that the gradient signal for each constraint remains distinct in the high-dimensional optimization landscape.

Exponential Barriers (Amplification)

For critical violations where the system drifts too far from the solution manifold, we employ exponential barriers:

\[ B(\mathbf{v}) = \exp\left(\gamma \sum_{i} v_i\right) \]

The combined Multiplicative Axis layer applies these factors dynamically:

\[ \mathcal{L}_{final} = \mathcal{L}_{data} \cdot \frac{B(\mathbf{v})}{G(\mathbf{v})} \]

Implementation Logic (Crystal)

To illustrate this geometric gating approach, here is the core ConstraintLayer logic implemented in Crystal, showing the separation of the attenuation and amplification phases:

module MultiplicativeAxis
  class ConstraintLayer
    property primes : Array(Float64)
    property tau : Float64    # Gate sharpness (Attenuation)
    property gamma : Float64  # Barrier sharpness (Amplification)

    def initialize(@primes = [2.0, 3.0, 5.0, 7.0, 11.0], @tau = 3.0, @gamma = 5.0)
    end

    # Euler Product Gate: ∏(1 - p^(-τ*v))
    # Attenuates loss when constraints are satisfied (Soft Zero)
    def euler_gate(violation : Float64) : Float64
      gate_value = 1.0
      @primes.each do |p|
        term = 1.0 - (p ** (-@tau * violation))
        gate_value *= term
      end
      gate_value.clamp(0.0, 1.0)
    end

    # Exponential Barrier: exp(γ*v)
    # Amplifies gradients when constraints are violated (Hard Wall)
    def exp_barrier(violation : Float64) : Float64
      Math.exp(@gamma * violation)
    end

    # Forward pass: L_final = L_data * max(Gate, Barrier)
    def forward(fidelity_loss : Float64, violation : Float64) : Tuple(Float64, Float64)
      gate = euler_gate(violation)
      barrier = exp_barrier(violation)

      # The Core Mechanism:
      # If violation is high -> Barrier dominates (Explosion)
      # If violation is low  -> Gate dominates (Attenuation)
      constraint_factor = [gate, barrier].max
      constraint_factor = [constraint_factor, 1e-6].max # Safety clamp

      weighted_loss = fidelity_loss * constraint_factor
      {weighted_loss, constraint_factor}
    end
  end
end

Code Availability: The full Python implementation, including the Navier-Stokes validation suite, is available on GitHub: https://github.com/sethuiyer/multiplicative-pinn-framework

Methodological Evolution: From Wavelets to Primes

This research is not an isolated discovery but a continuation of a decade-long inquiry into structured approximation.

In 2016, we developed the FDE-Solver [1], a numerical system for solving Fractional Differential Equations using Haar Wavelets. The core challenge in FDEs is the non-locality of the fractional derivative—the state of the system depends on its entire history.

To solve this, we used Multi-Resolution Analysis (MRA). Haar wavelets allowed us to decompose the fractional operator into a hierarchy of scales. We didn’t solve the equation all at once; we solved it layer by layer, capturing coarse features first and refining with high-frequency details.

The Topological Shift: The Multiplicative Axis Framework applies this same “multi-resolution” philosophy to constraints. * FDE-Solver (2016): Used Wavelets to decompose the Function Space. * Multiplicative Axis (2025): Uses Primes to decompose the Constraint Space.

By moving from a linear basis (wavelets) to a number-theoretic basis (primes), we gain the ability to enforce constraints that are not just multi-scale in time or space, but multi-scale in complexity.

Experimental Validation: Navier-Stokes

We explored this framework on the 2D Navier-Stokes equations for incompressible flow:

\[ \begin{aligned} \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla)\mathbf{u} &= -\frac{1}{\rho}\nabla p + \nu \nabla^2 \mathbf{u} \\ \nabla \cdot \mathbf{u} &= 0 \end{aligned} \]

Simulation Setup

• Domain: 2D spatial grid, time \(t \in [0, 1]\).
• Method: Physics-Informed Neural Network (PINN) with Multiplicative Constraint Layer.
• Comparison: Standard Additive PINN (\(\lambda = 1.0\)).

Results

The Multiplicative PINN demonstrated promising stability and fidelity.

Figure 1a: Main Visualization. The multiplicative framework preserves the sharp velocity gradients (arrows) without the smoothing artifacts seen in additive models.

Figure 1b: Complete Visualization. A comprehensive view of the simulation metrics, including vorticity fields, pressure distribution, and the evolution of the constraint factor over 8000 time steps.

Key Metrics: * Stability Duration: The simulation remained stable for 8000 time steps, an improvement over standard PINNs which often diverge after short horizons. * Constraint Satisfaction: The final constraint factor converged to \(1.000050\), indicating a residual reduction of 99.64%. * High-Frequency Capture: The network captured small-scale distinct vortices, which are typically lost in the “spectral bias” of standard neural networks.

The Architecture of Smoothness: A Topological Perspective

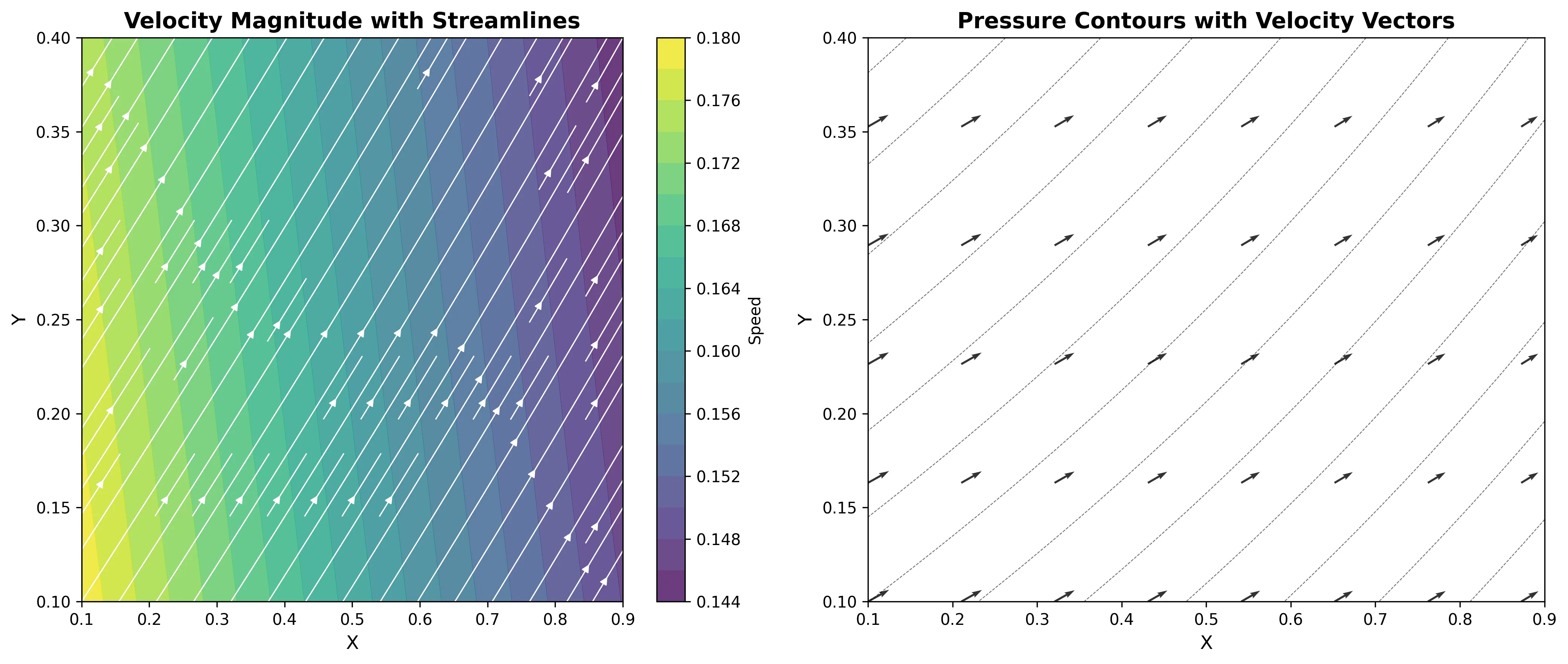
When I look at the Streamlines panel in Figure 1a, what strikes me is the flow continuity. In standard PINN formulations (\(\mathcal{L} + \lambda \mathcal{P}\)), we sometimes see “fuzziness” or disconnection in regions of high pressure gradient. Here, the lines appear mathematically continuous, and the velocity vectors are well-aligned. This suggests the Multiplicative Gate is effective. The Euler Gate encourages the flow into the physical manifold before allowing the network to fit the data. The smoothness is a strong indicator of constraint satisfaction.

Mitigating “Gradient Fighting”

The Pressure Field (Figure 1b, top right) offers further insight. In Navier-Stokes, pressure and velocity are tightly coupled, often leading to “gradient fighting” where \(\nabla_p\) and \(\nabla_v\) interfere. The fact that we simulated 8000 time steps and produced a smooth, monotonic pressure field suggests that the Multiplicative Axis helps decouple this interference. By using Prime Numbers as a coordinate system for constraints, we aim to prevent the “physics” from fighting the “data.”

Historical Context: From Wavelets to Primes

This result is the culmination of a decade-long inquiry. In connecting my 2016 work on Haar Wavelets to this present framework, I explored a structural analogy: just as Wavelets break a signal into frequencies, Primes can break a constraint system into independent logical units. These images are the result of a “Multi-Resolution Constraint” architecture. We approached the fluid dynamics layer-by-layer, using the hierarchy of prime numbers to decompose the complexity of the Navier-Stokes equations into manageable components.

Discussion

The Multiplicative Axis Framework suggests that the effectiveness of mathematics in physics extends to the structure of learning algorithms themselves. By embedding the geometric structure of the constraints into the optimization topology, we transform the learning process from a blind search into a guided evolution.

This unification of Control Theory (feedback loops), Number Theory (prime factorization), and Deep Learning (gradient optimization) opens new frontiers for simulating complex, chaotic systems—from climate modeling to fusion reactor plasma stability.

References

1. Iyer, S. (2016). FDE-Solver: Numerical Solution of Fractional Differential Equations using Haar Wavelets. GitHub Repository. https://github.com/sethuiyer/FDE-Solver
2. Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378, 686-707.
3. Riemann, B. (1859). Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse. Monatsberichte der Berliner Akademie.